PhilMath Intersem 3.2012
Theme
Complexities of Proof: Varieties, Effects & Management
Dates
June 6–June 26, 2012
Featured Speakers
Simon Colton (Computing, Imperial College London)
Patrick Dehornoy (Mathematics, U of Caen; CNRS)
Gilles Dowek (INRIA, Deducteam, Paris)
Benedikt Löwe (ILLC, U of Amsterdam; Mathematics,
U of Hamburg)
Ursula Martin (Computer Science, Queen Mary, U of
London)
Timothy McCarthy (Philosophy, U of Illinois–U/C)
Alison Pease (Computer Science, Queen Mary, U of
London)
Michael Rathjen (Pure Mathematics, U of Leeds)
Keith Stenning (Informatics & Computational Neuroscience, U of Edinburgh)
Claes Strannegård (Philosophy, Linguistics and Theory
of Science, U of Gothenburg)
Michiel van Lambalgen (ILLC, Philosophy, U of Amsterdam)
Andreas Weiermann (Mathematics, Ghent U)
Locations of Meetings
Meetings 1, 3, 7–10: Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Meeting 2 (June 8): Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Valentin (454A)
Meeting 4 (June 12): Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle 086A
Meetings 5, 6 (June 14, 15): Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Klimt (366A)
Maps & other info for Université de Paris 7–Diderot, Rive Gauche Campus and Bâtiment Condorcet.
Schedule of Meetings
Meeting 1: June 6, 14h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Pr. Ursula Martin, “1377 questions and counting – what can we learn from online math?”
Pr. Timothy McCarthy, “Induction, Confluence, and Underdetermination in Mathematics”
Meeting 2: June 8, 16h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Valentin (454A)
Pr. Keith Stenning, “Applying descriptive complexity theory to cognitive models of human reasoning, Part I”
Meeting 3†: June 9, 16h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
†: Saturday meeting
Pr. Michiel van Lambalgen, “Applying descriptive complexity theory to cognitive models of human reasoning, Part II”
Meeting 4: June 12, 14h00–16h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle 086A
Dr. Claes Strannegård, “Logical Reasoning with Bounded Cognitive Resources”
Meeting 5: June 14, 11h00–13h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Klimt (366A)
Pr. Benedikt Löwe, “Mathematical Knowledge by Testimony: the peer review process”
Meeting 6: June 15, 16h00–18h00. Université de Paris 7–Diderot, Bâtiment Condorcet, salle Klimt (366A)
Gilles Dowek, “The subformula property in logic, theories, and mathematics”
Meeting 7: June 18, 14h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Pr. Simon Colton, “Concept Formation with Proof in Mind”
Dr. Alison Pease, “Summary of an ethnographic study of the third Mini-Polymath Project”
Meeting 8: June 22, 16h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Pr. Michael Rathjen, “Long Proofs”
Meeting 9: June 25, 16h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Pr. Andreas Weiermann, “Proving mathematical results by believing in principles”
Meeting 10: June 26, 16h00–18h00. Université de Paris 7–Diderot, Rive Gauche Campus, Bâtiment Condorcet, salle Mondrian (646A)
Patrick Dehornoy, “The notion of truth in recent Set Theory, after Woodin"
Abstracts & Readings
Meeting 1: June 6th
1A Ursula Martin: “1377 questions and counting – what can we learn from online math?”
Abstract
Online blogs, question answering systems and distributed proofs provide a rich new resource for understanding what mathematicians really do, and hence for devising better tools for supporting mathematical advance.
In this talk we discuss the first steps in such a research programme, looking at two examples through a sociological lens, to see what we can learn about mathematical practice, and whether the reality of mathematical practice supports the theories of researchers such as Polya and Lakatos, or the expectations of computer scientists devising software to do maths.
Polymath provides a structured way for a number of people to work on a proof simultaneously: we analyse a polymath proof of a math olympiad problem to see what kinds of techniques the participants use. Mathoverflow supports asking and answering research level mathematical questions: we look at a sample of questions about algebra, and provide a typology of the kinds of questions asked, and consider the features of the discussions and answers they generate.
Finally we outline a programme of further work, and consider what our results tell us about mathematical practice, mathematical advance, and opportunities for further computational support for proof and question answering.
1B Timothy McCarthy: “Induction, Confluence, and Underdetermination in Mathematics”
Abstract
An ideal of reason is a norm to which an ideal cognizer would conform. An argument demonstrating that a number of such normative constraints are jointly incompatible could justly be called an antinomy of reason. In this note I am going to present an antinomy of reason stemming from a certain conception of mathematical knowledge, a conception articulated by Gödel in the Gibbs Lecture and later vigorously defended by Hilary Putnam (among others).
This conception is sometimes called quasi-empiricist, since there is assumed a given basis of mathematical data which lead, via an acceptable inductive method, to a generally non-monotonic epistemic evolution. There is some controversy about what these initial data should be taken to be. For my purposes, the only data assumed given are some rudimentary principles of elementary number theory; primitive recursive number theory or even Robinson's arithmetic will suffice.
The analogue of provability in this non-monotonic situation is a notion of stability: in the simplest case, where the epistemic evolution is ω-sequential, a content counts as stable at a given stage if it is projected therein and is retained at all subsequent stages. The main observation of this paper is that if the inductive method of an idealized agent satisfies a number of epistemologically well-motivated structural constraints, then the agent is incapable of effecting certain number-theoretic inductive inferences of the most elementary kind.
Suggested Reading
K. Gödel, “Some basic theorems on the foundations of mathematics and their implications”, in Kurt Gödel: Collected Works, vol. III, 304–324.
R. Jeroslow, “Experimental logics and $\Delta^0_2$ theories”, Journal of Philosophical Logic 4 (1975): 253–267
T. McCarthy, “Self-reference and incompleteness in a non-monotonic setting”, Journal of Philosophical Logic 23 (1994): 423–449
H. Putnam, “Trial and error predicates, and the solution to a problem of Mostowski”, Journal of Symbolic Logic 30 (1965): 49–57
Meeting 2: June 8th
[Note: Meetings 2 and 3 are two parts of a joint session. In the first part, Keith Stenning will introduce necessary cognitive background. In the second part, Michiel van Lambalgen will make a case that descriptive complexity theory (as developed in finite model theory) can explain even fine-grained observed differences in complexity between different pieces of reasoning.]
Keith Stenning: “Applying descriptive complexity theory to cognitive models of human reasoning. Part I”
Abstract, Part I
It is a commonplace that alternative representations of problems can have profound effects on their complexity of solution. (Stenning, 2002) sought a framework for the empirical study of how diagrammatic vs. sentential representation affects the relative complexity of some elementary deductive proofs, and thence the cognitive consequences of using them in
teaching/learning/reasoning about elementary logic.
(Stenning & Lambalgen, 2008) presents an argument that the supposedly classical logical tasks of the deductive reasoning lab invoke a variety of interpretations in the reasoners observed, which can explain the apparent irrationality of subjects’ reasoning.
This talk will introduce the arguments and some of the empirical results,
and problems with explaining them, setting the scene for the second talk to explore specific examples.
Suggested Reading
K. Stenning, Seeing Reason (OUP 2002), chapters 1 and 4.
K. Stenning & M. van Lambalgen, Human reasoning and cognitive science (MIT 2008), chapters 3 and 4.
Meeting 3: June 9th
Michiel van Lambalgen: “Applying descriptive complexity theory to cognitive models of human reasoning. Part II”
Abstract, Part II
One example concerning fine-grained differences in complexity of reasoning
comes from the Wason selection task. This is a conditional reasoning task in which, in a typical subject group, only around 5% arrive at the answer mandated by classical logical interpretation.
This result has led to reactions such as: subjects don’t reason logically, but probabilistically (Oaksford & Chater, 2007); evolution has not equipped us with a general purpose reasoning capacity (Cosmides & Tooby, 2004); or peoples’ reasoning is driven by content not by form (Johnson-Laird & Byrne, 1991)).
In this talk we look at the selection task from the standpoint of finite model theory, i.e. descriptive complexity. There are various versions of the task, some of which are easy for subjects (75% correct). We show (i) that the standard version of the task asks a subject to prove a 
statement, (ii) that the explicit introduction of excluded middle as an ideal element lowers the complexity somewhat, resulting in better scores, (iii) that subjects’ own attempts at lowering complexity involve changing the meaning of the conditional, and (iv) that the easy version of the selection task corresponds to proving a first order theorem. The real complexity barrier is thus between
first and second order.
Suggested Reading
Cosmides, L., & Tooby, J. (2004). Social exchange: the evolutionary design of a neurocognitive system. In M. Gazzaniga (Ed.), The cognitive neurosciences iii (pp. 1295–1308). MIT.
Johnson-Laird, P. N., & Byrne, R. (1991). Deduction. Hove, Sussex.: Lawrence Erlbaum Associates.
Oaksford, M., & Chater, C. (2007). Bayesian rationality: The probabilistic approach to human reasoning. Oxford: Oxford University Press.
K. Stenning, Seeing Reason (OUP 2002), chapters 1 and 4.
K. Stenning & M. van Lambalgen, Human reasoning and cognitive science (MIT 2008), chapters 3 and 4.
Meeting 4: June 12th
Claes Strannegård: “Logical Reasoning with Bounded Cognitive Resources”
Abstract
Results from cognitive psychology indicate that cognitive resources such as sensory memory, working memory, and declarative memory are (i) bounded in their capacity and (ii) critical for problem solving in a wide range of domains, including formal logic.
First, I propose a strategy for modeling problem solving with bounded cognitive resources in formal logic. More precisely, I propose a proof formalism that includes logical inference rules as well as explicit models of certain cognitive resources. By putting capacity limits on the latter, various notions of resource-bounded provability can be obtained.
Secondly, I report the results of three empirical studies in deductive reasoning, in which data concerning accuracy and latency was collected in psychological experiments. The empirical studies concern validity in propositional logic, truth
in first-order logic with respect to finite graphs, and evaluation of arithmetical expressions, respectively.
In each of these cases, a specific resource-bounded proof system was constructed together with a computer program for generating proofs in this system and finding the length of the shortest proofs and the size of the smallest proofs of a given sentence. This makes it possible to compare mathematical complexity measures (such as minimum proof length) with
psychological complexity measures (such as latency) and perform statistical analyses of their correlations.
Suggested Reading
C. Strannegård, S. Ulfsbäcker, D. Hedqvist and T. Gärling, “Reasoning Processes in Propositional Logic”, Journal of Logic, Language & Information 19 (2010): 283–314 [Available online at: Reasoning in Propositional Logic]
Meeting 5: June 14th
Benedikt Löwe: “Mathematical Knowledge by Testimony: the peer review process”
Abstract
Mathematics has been described as a building where each statement rests on countless others; these others have been confirmed by the method of proof. Or, at least in theory; in practice, they have been confirmed by a mixture of community consensus and the peer review process. What is the relationship between proof on the one hand and the methods actually employed by the mathematical community to check the correctness of theorems?
In this talk, we’ll give a description of the peer review process and discuss how to approach it to gain insights into mathematical proof-making.
Suggested Reading
C. Geist, B. Löwe & B. Van Kerkhove, “Peer review and knowledge by testimony in mathematics”, in Philosophy of Mathematics: Sociological Aspects and Mathematical Practice (2010), College Publications: 155–178. [Online at PhiMSAMP.]
B. Löwe & T. Müller, “Data and phenomena in conceptual modelling”, Synthese 182 (2011): 131–148. [Online at: Data and Phenomena.]
Meeting 6: June 15th
Gilles Dowek: “The subformula property in logic, theories, and mathematics”
Abstract
The subformula property expresses that, in a proof, we may avoid using concepts that are not explicit in the proved statement. This theorem of logic contradicts our experience of mathematics, where most proofs use extraneous concepts. This contradiction can be explained by the fact that mathematical proofs are not purely logical but are theoretical and theories affect the very notion of subformula. On the positive side, this impact on the notion of formula can be used to classify theories.
Meeting 7: June 18th
7A. Simon Colton: “Concept Formation with Proof in Mind”
Abstract
Certain types of concepts lend themselves more easily to the formation of conjectures that can be proved. For instance, we can prove conjectures in group theory where all pairs of elements commute (Abelian groups), or where no pair of elements commute (namely their nonexistence), but we find it difficult to prove theorems about groupswhere 25% of pairs of elements
commute.
Our HR automated theory formation system originally started life as software able to form theories in domains of pure mathematics, and its concept formation techniques were tailored to producing empirically plausible conjectures, the truth of which would follow deductively from
the axioms of the domain it was working in. Due to this nature, HR has discovered some theorems in number theory and domains of finite algebra worthy of publication in the mathematical literature. However, as HR has developed into a more general machine learning system able to discover empirically plausible conjectures about data of a more generic nature (where there are often no underlying axioms to refer to, or the discovery of the axioms is the name of the game), the concept formation techniques have likewise developed.
In the talk, I will chart the history of concept formation in the HR system through the prism of the possibilities (or lack thereof) for proving conjectures which relate the concepts.
7B. Alison Pease: “Summary of an ethnographic study of the third Mini-Polymath Project”
Abstract
In his article ’Computing Machinery and Intelligence’, Alan Turing proposed to consider the question, “Can machines think?”. We consider the question, “Can machines do mathematics, and how?”
Turing suggested that intelligence be tested by comparing computer behaviour to human behaviour in an online discussion. We hold that this approach could be useful for assessing computational logic systems which, despite having produced formal proofs of the Four Colour Theorem, the Robbins Conjecture and the Kepler Conjecture, have not achieved widespread takeup by mathematicians.
It has been suggested that this is because computer proofs are perceived
as ungainly, brute-force searches which lack elegance, beauty or mathematical insight. One response to this is to build such systems which perform in a more human-like manner, which raises the question of what a “human-like manner” may be.
Timothy Gowers recently initiated Polymath, a series of experiments in online collaborative mathematics, in which problems are posted online, and an open invitation issued for people to try to solve them collaboratively, documenting every step of the ensuing discussion. The resulting record provides an unusual example of fully documented mathematical activity leading to a proof, in contrast to typical research papers which record proofs, but not how they were obtained.
We consider the third Mini-Polymath project, started by Terence Tao and published online on July 19, 2011. We examine the resulting discussion from the perspective: what would it take for a machine to contribute, in a human-like manner, to this online discussion? We present an account of the mathematical reasoning behind the online collaboration, which involved about 150 informal mathematical comments and led to a proof of the result. We distinguish four types of comment, which focus on mathematical concepts, examples, conjectures and proof strategies, and further categorise ways in which each aspect developed.
Where relevant, we relate the discussion to theories of mathematical practice, such as those proposed by Polya and Lakatos, and consider how their theories stand up in the light of this documented record of informal mathematical collaboration. We briefly discuss automated systems which currently find examples, form concepts and conjectures, and generate proofs; and conclude that Turing was right when he commented: “We can only see a short distance ahead, but we can see plenty there that needs to be done.”
Meeting 8: June 22nd
Michael Rathjen: “Long proofs”
Abstract
Gödel showed that a system S of higher order can prove theorems that a system T of lower order cannot. He also showed that there are theorems θ that both S and T can prove but where a proof of θ in S is much shorter than the shortest proof of in T.
In proof theory there are many results where a system S is reduced to another system T, i.e. it is shown that S is conservative over T with respect to 
or arithmetic theorems.
Another important technique of proof theory is concerned with extracting numerical bounds from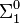 
theorems. The two techniques can be combined to show that there are specific 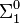theorems that have short proofs in a system S but only extremely long proofs in a system T.
To arrive at that conclusion, however, requires an investigation of how infinitary proof theory with its use of infinite proof trees yields finitistic conservativity results.
Suggested Reading
P. Pudlak, “The length of Proofs”, in Handbook of Proof theory (1998), Elsevier: 547–637
S. G. Simpson, “Nonprovability of certain combinatorial properties of finite trees”, in Harvey Friedman’s Research on the Foundations of Mathematics (1985): 87–117
R. Smith, “The consistency strength of some finite forms of the Higman and Kruskal theorems”, in Harvey Friedman’s Research on the Foundations of Mathematics (1985): 119–135
Meeting 9: June 25th
Andreas Weiermann: “Proving mathematical results by believing in principles”
Abstract
In this talk I will speak about some general principles in which I believe. These principles are certain forms of conjectures which are too general to be formulated as a definite statement which could be proved. I will indicate how I use these principles to prove research results.
These principles are speculative in nature but they proved to be unreasonably effective in predicting claims which often could be proved afterwards. Such principles are particularly useful when one deals with complex situations in proof theory. Notions like Naturalness and Beauty play an important role in this approach.
Another facet is that nice results should emanate from nice structures. (My personal belief is that Harvey Friedman’s work is a primary source to look
for.) I will underpin my speculations with concrete examples. Interested PhD students (and other people) are invited to test out these principles at their own
(at their own risk).
Suggested Reading
A. Weiermann, “Proving termination for term rewriting systems”, Lecture Notes in Computer Science 1992, vol. 626/1992: 419–428
A. Weiermann, “A Computation of the Maximal Order Type of the Term Ordering on Finite Multisets”, Lecture Notes in Computer Science 2009, vol. 5635: 488–498
A. Weiermann, “Phase Transition Thresholds for Some Natural Subclasses of the Computable Functions”, Lecture Notes in Computer Science 2006, vol. 3988: 556–570
A. Weiermann, “Analytic combinatorics, proof-theoretic ordinals, and phase transitions for independence results”, Annals of Pure and Applied Logic 136 (2005): 189–218
Meeting 10: June 26th
Patrick Dehornoy: “The notion of truth in recent Set Theory, after Woodin”
Abstract: Building on a description of some recent advances in post-Cohen Set Theory, we shall discussWoodin’s position claiming that an axiom can be validated on the basis of an a posteriori interiorisation of its usefulness and eventually be considered to be true (without quotes). One of the facets of the discussion could be Woodin’s refutation of Hamkins’ Multiverse approach
because it violates some natural complexity postulate.
Participants
Aldo Antonelli (U of California–Davis)
Andrew Arana (U of Illinois–U/C)
Pascal Bertin (U of Paris 7)
Matteo Bianchetti (U of Notre Dame)
Julien Boyer (U of Paris 1; IHPST)
Sylvain Cabanacq (ENS, U of Paris 7)
Méven Cadet (U of Paris 1; IHPST)
Karine Chemla (CNRS; Rehseis/Sphere)
Joao Cortese (U of Paris 7)
Davide Crippa (U of Paris 7)
Michael Detlefsen (U of Notre Dame)
Elias Fuentes (U of Paris 1; IHPST)
Henri Gallinon (U of Paris 1; IHPST)
Fernando Galvez (U of Paris 1; IHPST)
Emmylou Haffner (U of Paris 7)
Ramzi Kebaili (U of Paris 7)
Elaine Landry (U of California–Davis)
Graham Leach-Krouse (U Notre Dame)
Clarissa Lee (Duke U)
Corentin Le Fur (U of Paris 7)
Didier Lesesvre (U of Paris 7)
Marco Panza (CNRS; U of Paris 1; IHPST)
Mattia Petrolo (U of Paris 7)
Francesca Poggiolesi (Paris 1; IHPST)
Chris Porter (U of Notre Dame)
David Rabouin (CNRS; Rehseis/Sphere)
Mathys Rennela (U of Paris 7)
Ivahn Smadja (Paris 7; Rehseis/Sphere)
Tony Strimple (U of Notre Dame)
Jean-Jacques Szczeciniarz (U of Paris 7)
Justin Taylor (U of Notre Dame)
Sean Walsh (Birkbeck, UC–Irvine)
Participation Welcome
All interested persons are encouraged to participate. If you have questions, please contact Mic Detlefsen or Emmylou Haffner.
PhilMath Intersem 2012 is a joint cooperation of the University of Notre Dame, the Université de Paris 7–Diderot, the Université de Paris 1 (IHPST), the ENS and the Université de Lorraine.